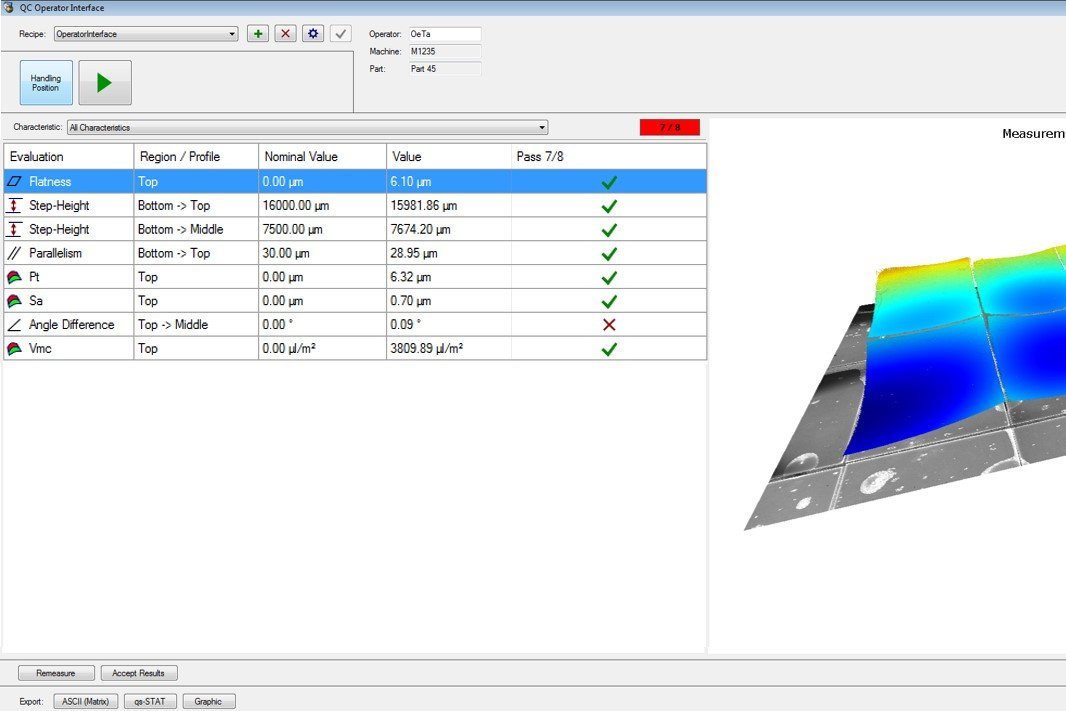
Warum die Ebenheit von Oberflächen messen?
Ebenheitstoleranzen werden als Qualitätsindikator vieler Produktionen herangezogen, weil die Ebenheitsauswertung für viele Anwendungen entscheidend ist hinsichtlich Funktionalität technischer Komponenten. Die Ebenheit als Oberflächenparameter beeinflusst z. B. die Leckage von Dichtflächen an Flanschen und Ventilsitzen. Die Ebenheit von Oberflächen kann auch den Geräuschpegel und die Schallemission von Bauteilen beeinflussen. In der Präzisionsoptik, oftmals unter Einsatz optischer Polierverfahren, gilt die Ebenheit von Glassubstraten z. B. für Bauteile wie optische Spiegel oder Strahlteiler als einer der wichtigsten Qualitätsindikatoren. Auch außerhalb der Feinmechanik und optischen Komponenten sind Ebenheitstoleranzen weit verbreitet. In der Elektronikindustrie ist es wichtig zu wissen, ob die Ebenheit von Leiterplatten innerhalb der spezifizierten Toleranzen liegt, um die elektrische Verbindung zu gewährleisten, wenn mehrere Teile z. B. per Lötstellen verbunden sind. Einfach ausgedrückt: Ebenheitstoleranzen haben großen Einfluss auf die Zuverlässigkeit und Funktionalität in der industriellen Produktion.
Kostenfreie Machbarkeitsstudie anfordern zur Ebenheitsmessung Ihrer Prüflinge!
Wir messen die Ebenheit an Ihren Prüflingen - vor Ort oder online
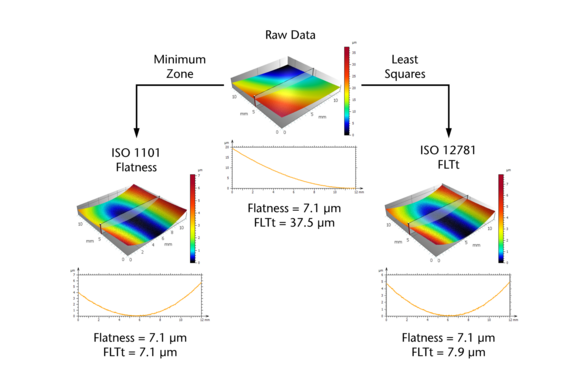
Ebenheit nach ISO und wie Ebenheit berechnet wird
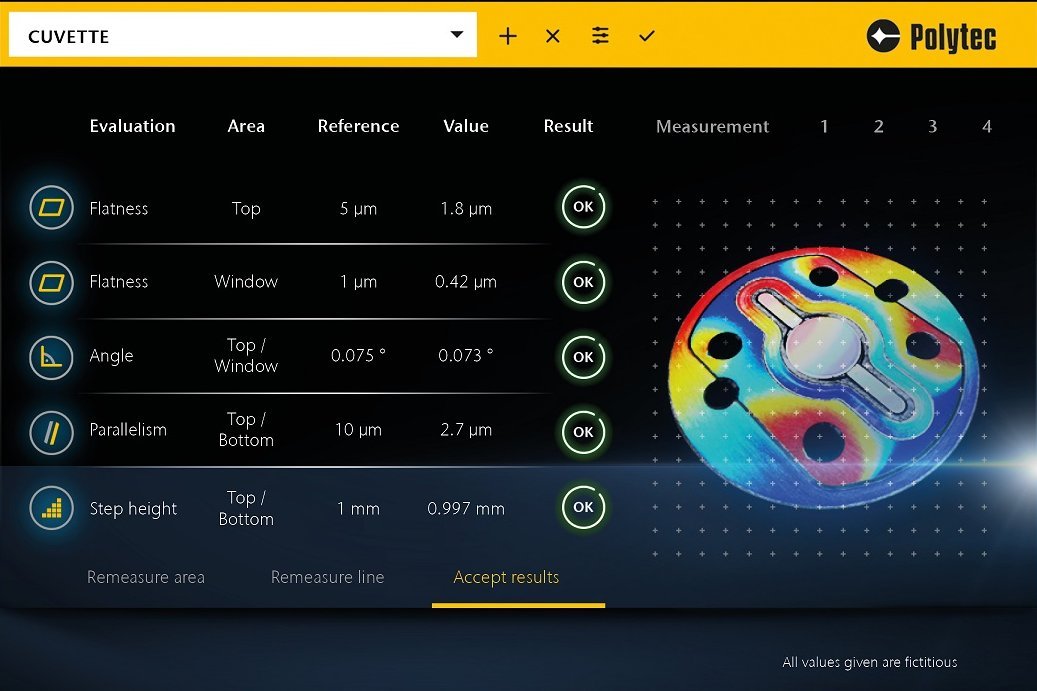
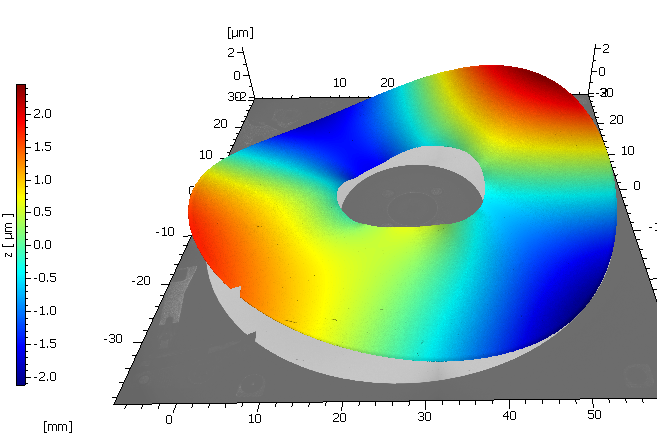
Im Allgemeinen wird die geometrische Ebenheit in der Messtechnik als die Differenz zwischen zwei parallelen Ebenen über alle erfassten Messpunkte definiert. Es gibt jedoch verschiedene ISO-Normen, die sich darin unterscheiden, wie diese parallelen Ebenen zu berechnen sind. Um die Ergebnisse von Ebenheitsmessungen mit verschiedenen Messsystemen und -technologien vergleichen zu können, ist es wichtig, sich auf eine bestimmte ISO-Norm zu beziehen. Die ISO-Norm 1101 legt fest, dass der Abstand zwischen zwei parallelen Ebenen so klein wie möglich sein muss, wobei alle Messpunkte einbezogen werden. In der ISO-Norm 12781 wird die Ebenheit viel allgemeiner als Abstand zwischen dem minimalen und dem maximalen Punkt zweier Ebenen definiert, wobei der Abstand von den zuvor vorgenommenen Formabnahmen abhängt. Unabhängig von der verwendeten ISO-Norm ist es wichtig, Ausreißer im Datensatz wirksam zu eliminieren, um zu verhindern, dass einzelne Spitzen das Messergebnis dominieren.
Vorteile der optischen Ebenheitsmessung
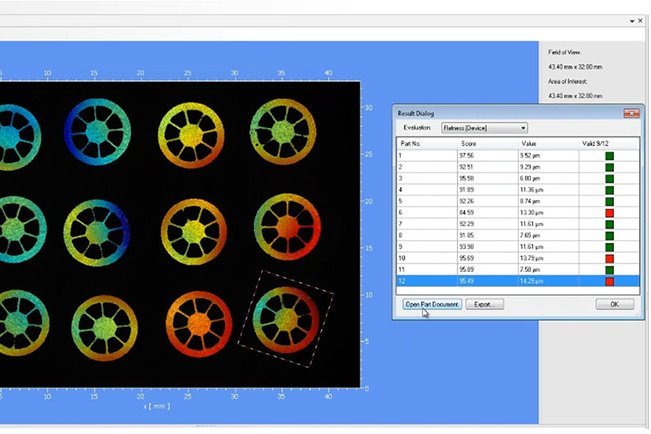
Ebenheitsmessungen werden in der Regel entweder mit taktilen Profilmessgeräten oder berührungslos optisch durchgeführt. Taktile Messsysteme wie Koordinatenmessgeräte (KMG) werden häufig für die Ebenheitsmessung großer Teile verwendet, bei denen mehrere Maß-, Geometrie- oder Positionswerte bewertet werden sollen. Koordinatenmessgeräte führen typischerweise zu sehr langen Messzeiten, da es sich um eine Punkt-für-Punkt-Messung handelt. Wählt man größere Punktabstände, kann die Messzeit reduziert werden. Damit wird allerdings in Kauf genommen, dass lokale Formabweichungen übersehen werden.