レーザドップラ振動計とは
レーザドップラ振動計は変位および速度を高分解能で測定する最良の方法で、多くの基礎科学分野で使用されています。その振幅分解能はフェムトメートルを実現しており、線形性に優れ、従って6GHz以上に達する非常に高い周波数帯域まで測定できます。測定距離は可変であり、最小は顕微鏡サイズから最大は百メートルに及びます。レーザを照射しても測定物に影響を与えず、極めて小さくて軽量な構造物も測定することができます。また頑丈な設計を施しているので、屋内でも屋外でも使用可能です。
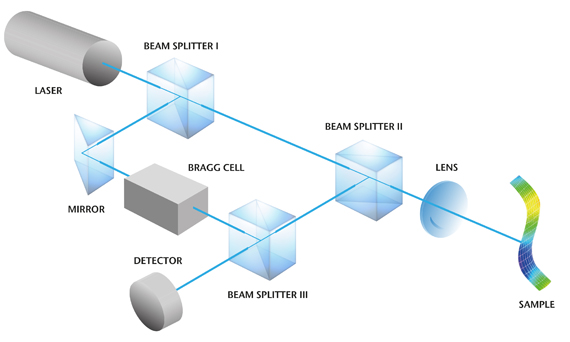
レーザドップラ振動計の測定原理
小型軽量物の微細な振動を非接触で測定
小型軽量構造物の非接触特性評価。振動、音響、動的挙動の解析。生物・医療系の生体、エレクトロニクス部品、MEMSなどの小型で軽量な測定物も、質量負荷なくレーザで、非接触で測定できます。レーザドップラ振動計は、測定周波数帯域がDCからGHzまでと広く、振動モード・周波数応答を測定し、解析結果の検証ができます。共振周波数、インパルス応答、減衰特性を測定します。微細な振動も、ポリテックのレーザドップラ振動計なら測定できます!
レーザドップラ振動計の無料デモやフィジビリティスタディをご体験ください!
QTec® マルチパス干渉計を搭載したレーザドップラ振動計
QTec® レーザドップラ振動計は、ノイズの根本原因を排除することで、レーザドップラ振動計の常識を覆し、あらゆる表面で優れた光学感度と高精度な測定を実現します。ポリテックの QTec レーザドップラ振動計は、革新的なマルチパス干渉計コンセプトを採用。この特許技術に、実績のある赤外線センサ Xtra を組み合わせることで、より迅速で容易な測定と、安定した測定結果を実現しています。

ドップラ効果
振動するオブジェクトから反射した光の波を LDV で測定するとき、測定した波の周波数シフトは次の式で表されます。
fD = 2· v/λ
「v」 は振動するオブジェクトの速度、「λ」 は照射された光の波長です。オブジェクトの速度を知るには、(ドップラ)周波数シフトを既知の波長で測定する必要があります。これは、レーザドップラ振動計(LDV)においてはレーザ干渉計によって測定できます。
干渉計
LDV は、光学干渉に基づき計測します。光学干渉では、重ね合わせに 2 本の可干渉性のビームが必要であり、それぞれの光の強度を 「I1」 および 「I2」 とします。求められる強度は各ビームの強度の和ではなく、いわゆる 「干渉項」 を含む次の式によって変調されます。
Itot = I1 + I2 + 2 √(I1 I2 cos [2π(r1 - r2)/λ]
この干渉項は、両ビームの光路の長さの差に関係します。この差がレーザ波長の整数の積であるとき、全体の強度は単一のビームの 4 倍になります。 またしたがって、両ビームの光路の差が、1 つの波長の半分であるとき、全体の強度はゼロになります。
ドップラシフト周波数
単位時間当たりの光路長の変化は、測定ビームのドップラ周波数として現れます。これは、測定された干渉縞の変調周波数が、オブジェクトの速度に正比例することを意味します。干渉縞 (および周波数シフト) は、オブジェクトが干渉計から遠ざかるときも、逆にオブジェクトが干渉計に近づくときも全く同じのため、干渉縞だけではどちらの方向に動いているのかを判断することはできません。これを判断するため、参照ビームの光路上に ブラッグセル と呼ばれる音響光学変調器が設けられています。ブラッグセル により、光の周波数は 40 MHz シフトします (ちなみにレーザ光の周波数は 4.74 x 1014 Hz です)。このため、オブジェクトが静止状態のとき、干渉縞に 40 MHz の変調周波数が発生します。オブジェクトが干渉計に近づくとき、この変調周波数は 40 MHz よりも高くなります。逆に遠ざかるときは、40 MHz よりも小さくなってディテクタで検出されます。これにより、振動の振幅量だけでなく、オブジェクトがどちらの方向に振動しているのかも明確に検知できます。
変位と速度
LDV は速度と同様に変位も直接測定できます。この場合、ドップラ周波数は速度に比例する電圧には変換されず、かわりに LDV はディテクタ上の明暗の縞をカウントします。最適な補間方法を採用することにより、ポリテックの LDV は 2 nm という微細な振幅分解能で収集でき、さらにデジタル復調技術を用いる場合にはピコメータ レンジまで実現できます。なお、調和振動の最大振幅は次の式で表されるため、変位の復調は周波数が低いほど、速度の復調は周波数が高いほど適しています。
v = 2π • f • s
振動は、周波数が高くなるほど速度が速くなり、変位振幅は小さくなります。



